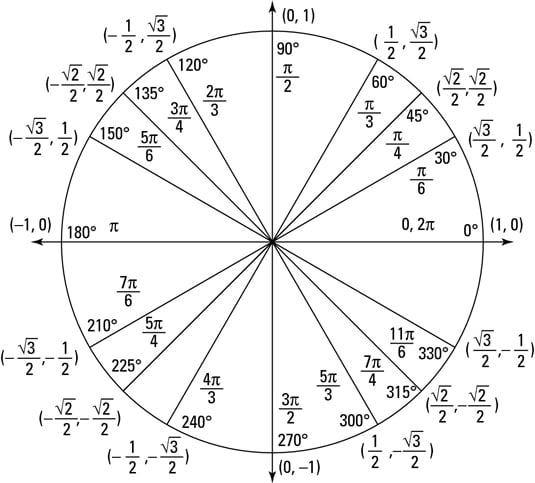
The unit circle also has applications in calculus, particularly in the study of limits and derivatives of trigonometric functions. In this essay, we will discuss the use of the unit circle in calculus.
Definition of Limits:
In calculus, a limit is a mathematical concept that describes the behavior of a function as the input variable approaches a certain value.
The limit of a function f(x) as x approaches a is denoted by:
lim f(x) = L x → a
If the function approaches the same value L from both sides of a, then the limit exists at a. The unit circle is used to evaluate the limits of trigonometric functions as the input variable approaches certain values.
Evaluation of Limits of Trigonometric Functions:
The limits of trigonometric functions can be evaluated using the unit circle. For example, consider the limit of the sine function as x approaches 0. Using the unit circle, we know that sin(0) = 0. Therefore, the limit of sin(x) as x approaches 0 is also 0.
Similarly, the limit of the cosine function as x approaches 0 can also be evaluated using the unit circle. Using the unit circle, we know that cos(0) = 1. Therefore, the limit of cos(x) as x approaches 0 is also 1.
Derivatives of Trigonometric Functions:
The unit circle is also used to derive the derivatives of trigonometric functions. The derivatives of the trigonometric functions are defined as follows:
- d/dx sin(x) = cos(x)
- d/dx cos(x) = -sin(x)
- d/dx tan(x) = sec^2(x)
- d/dx csc(x) = -csc(x) cot(x)
- d/dx sec(x) = sec(x) tan(x)
- d/dx cot(x) = -csc^2(x)
The unit circle can be used to prove these derivative formulas.
For example, consider the derivative of the sine function.
Let P(x, y) be a point on the unit circle corresponding to the angle x. Then, we can express sin(x) as the y-coordinate of P(x, y). To find the derivative of sin(x), we need to find the derivative of the y-coordinate of P(x, y) with respect to x. This derivative is equal to the x-coordinate of the unit tangent vector to the unit circle at P(x, y), which is equal to cos(x).
Therefore, we have:
d/dx sin(x) = d/dx y-coordinate of P(x, y) = x-coordinate of the unit tangent vector to the unit circle at P(x, y) = cos(x).
Similarly, the derivatives of the other trigonometric functions can be derived using the unit circle.
FAQ's on Unit Circle in Calculus
Here are some frequently asked questions related to the unit circle in calculus:
How is the unit circle used in calculus?
The unit circle is used in calculus to define the values of the trigonometric functions in terms of their Taylor series expansions. These series are used to approximate the values of the functions for any value of the argument (i.e., the angle) and to evaluate integrals and solve differential equations involving the functions.
What is the relationship between the unit circle and the Taylor series expansions of the trigonometric functions?
The Taylor series expansions of the trigonometric functions are defined in terms of the coordinates of points on the unit circle. Specifically, the coordinates of a point (x,y) on the unit circle with argument θ are given by x = cos(θ) and y = sin(θ). By expressing the functions as series of terms involving these coordinates, we can relate the values of the functions to the argument.
How do you use the unit circle to find the Taylor series expansion of a trigonometric function?
To use the unit circle to find the Taylor series expansion of a trigonometric function, you start by expressing the function as a series of terms involving powers of the argument and the coefficients of the terms. You then use the coordinates of points on the unit circle to express these coefficients in terms of factorials and powers of π. The resulting series gives an infinite sequence of terms that can be used to approximate the value of the function for any value of the argument.
What are some applications of the unit circle in calculus?
The unit circle and its relationship with the trigonometric functions are used in many applications of calculus, such as the evaluation of integrals and the solution of differential equations involving trigonometric functions. In addition, the unit circle is used to define the values of the complex exponential function, which is a fundamental function in many areas of mathematics and physics.
How does the unit circle relate to complex numbers?
The unit circle is closely related to complex numbers, which are numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit (i.e., the square root of -1). Specifically, the coordinates of a point (x,y) on the unit circle can be written as x + yi, which is a complex number of magnitude 1. The complex exponential function, which is defined in terms of the unit circle, is used extensively in the study of complex analysis and other areas of mathematics and physics.
What are some common mistakes to avoid when using the unit circle in calculus?
One common mistake is to confuse degrees and radians when working with the unit circle. Another mistake is to confuse the values of the sine and cosine functions when evaluating integrals or solving differential equations. It is also important to be careful when using the Taylor series expansions of the functions, as these series may converge only for certain values of the argument.
Conclusion:
In conclusion, the unit circle is an essential tool in calculus that is used to evaluate the limits of trigonometric functions and derive their derivatives. The use of the unit circle makes it possible to simplify the calculations involved in finding the derivatives of trigonometric functions, as the derivatives can be expressed in terms of the coordinates of the point on the unit circle corresponding to the angle x.
The unit circle is a powerful tool that has several applications in various fields, including mathematics, physics, and engineering.